Venn-Diagramm: Ein umfassendes Tutorial

Venn-Diagramme  sind grafische oder bildliche Darstellungen von Beziehungen zwischen verschiedenen Gruppen von Dingen. Das Venn-Diagramm wurde um 1880 von John Venn erfunden. Venn-Diagramme werden auch Mengendiagramme genannt. Venn-Diagramme geben eine logische Darstellung der Gruppen oder Mengen. Beziehungen zwischen zwei oder drei Mengen können mit Hilfe von Venn-Diagrammen leicht verstanden werden. In der Mathematik werden Venn-Diagramme verwendet, um bekannte Informationen aus Umfragen, Datenberichten und Tabellen zu analysieren.

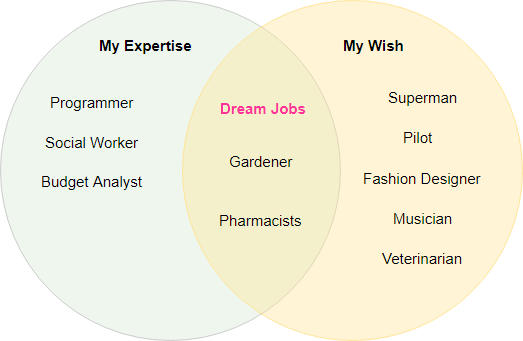
Zweck von Venn-Diagrammen

• Venn-Diagramme sind effektiv, um die Ähnlichkeiten oder Unterschiede zwischen mehreren Datensätzen (normalerweise zwei bis vier) anzuzeigen.
• Venn-Diagramme beschreiben auch das Ergebnis der Vereinigung mehrerer Datengruppen.
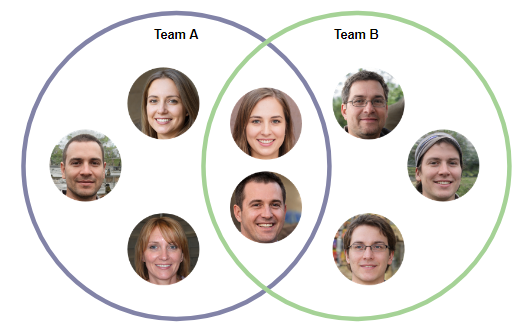
• Sie können auch die sich überschneidenden Verantwortlichkeiten zweier Organisationen/Teams beschreiben.

Venn-Diagramme einkreisen

Venn-Diagramme verwenden Kreise, um Mengen darzustellen und die Beziehung zwischen einer endlichen Sammlung verschiedener Mengen zu veranschaulichen. In der Mathematik werden Venn-Diagramme verwendet, um bekannte Informationen aus Umfragen, Datenberichten und Tabellen zu analysieren, die aus mehreren überlappenden geschlossenen Kurven bestehen, normalerweise Kreisen, die jeweils einen Satz darstellen.

Zum Beispiel:

• Menge natürlicher Zahlen = {1,2,3,…..}
• Menge ganzer Zahlen = {0,1,2,3,…..}
• Jedes Objekt wird als Element der Menge bezeichnet.

Die folgenden Beispiele zeigen die grundlegenden Operationen von set in Bezug auf Venn-Diagramme.

Set Basic OperationsVenn-Diagramm Der Schnittpunkt zweier Sets A ∩B = ist die Anzahl der Elemente, die sowohl in den Sets A als auch in B vorhanden sind.

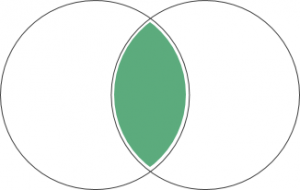
Vereinigung zweier Mengen AUB = ist die Anzahl der Elemente, die in einer der Mengen A oder B vorhanden sind.

Symmetrische Differenz von zwei

Beispiele für Venn-Diagramme

Venn-Beispiel: Klasse von Studenten

In einer Klasse mit 100 Schülern mögen 35 Naturwissenschaften und 45 Mathematik. 10 wie beide. Wie viele mögen einen von beiden und wie viele mögen keinen von beiden?

• Gesamtzahl der Studierenden, n(µ) = 100
• Anzahl der Studierenden der Naturwissenschaften, n(S) = 35
• Anzahl der Mathematikstudenten, n(M) = 45
• Anzahl der Schüler, die beides mögen, n(M∩S) = 10
• Anzahl der Schüler, die beide mögen,
• n(MᴜS) = n(M) + n(S) — n(M∩S)
• → 45+35–10 = 70
• Anzahl der Schüler, die beides nicht mögen = n(µ) — n(MᴜS) = 100–70 = 30

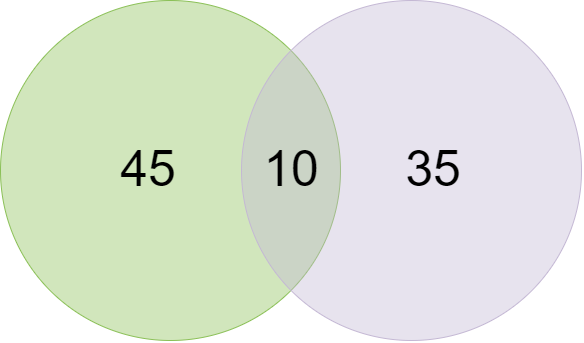
Bearbeiten Sie dieses Venn-Diagramm

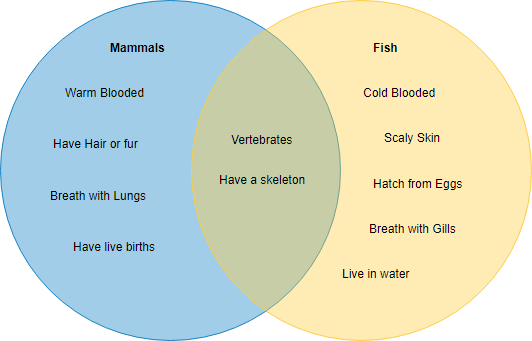
Beispiel eines Venn-Diagramms: Säugetiere und Fische

Dies ist ein Beispiel für ein Venn-Diagramm, das die Merkmale von Säugetieren und Fischen zeigt, die als zwei Ovale gruppiert sind. Die gemeinsamen Merkmale werden innerhalb des Überlappungsbereichs der beiden Ovale platziert.

Bearbeiten Sie dieses Venn-Diagramm

Venn-Diagramm mit drei Kreisen

Ein 3-Kreis-Venn-Diagramm ist eine Möglichkeit, Gruppen von Objekten mit denselben Eigenschaften zu klassifizieren.

• Es hat drei Kreise, die sich schneiden.
• Jeder Kreis hat seine eigenen Eigenschaften von Dingen, die in den Kreis passen, zB ungerade Zahlen oder Formen mit rechten Winkeln.
• Es gibt auch einen Raum außerhalb der Kreise, in den Objekte, die zu keiner der Eigenschaften passen, gehen können.
• Das folgende Diagramm zeigt Ihnen, wie ein Venn-Diagramm mit 3 Kreisen funktioniert.

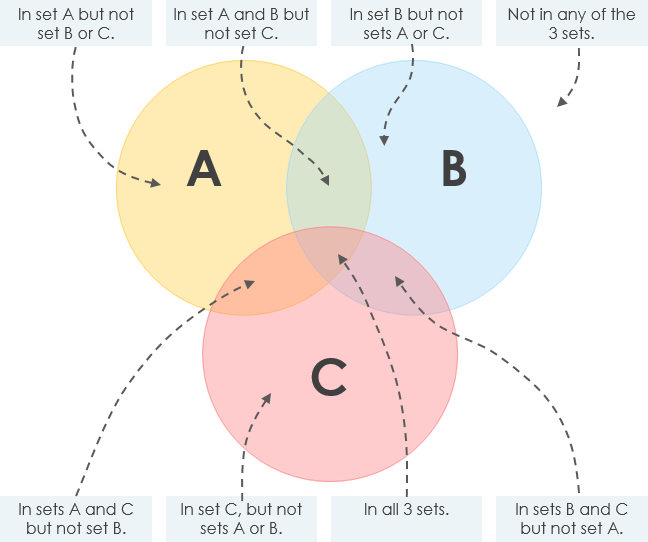
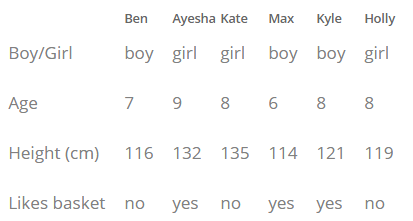
Das folgende Beispiel veranschaulicht das Konzept des obigen Satzes.

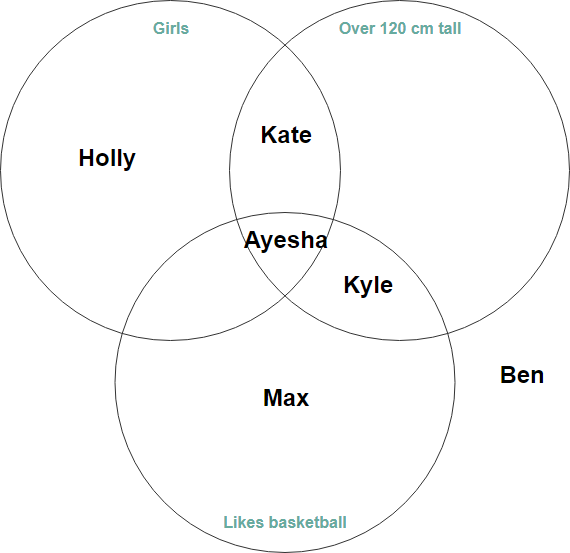
Bearbeiten Sie dieses Venn-Diagramm

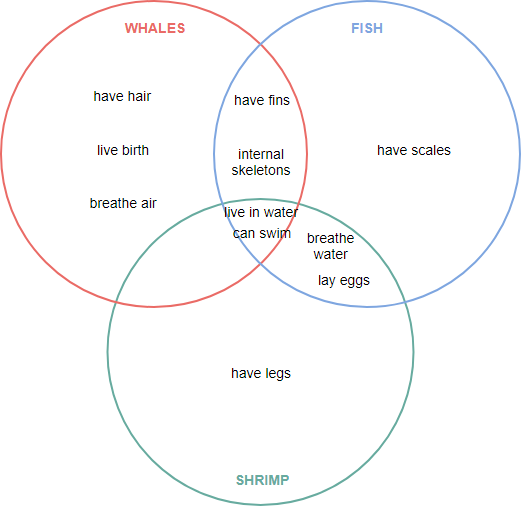
3 Beispiel für ein Kreis-Venn-Diagramm – Wasserlebewesen

Durch die Erweiterung des obigen Beispiels zeigt dieses Venn-Diagramm Beziehungen zwischen aquatischen Lebensformen: Wale (Säugetiere) und Fische, Garnelen (Wasserlebewesen). Auf den verschiedenen Feldern sind charakteristische Wasserlebewesen. In den Überlappungen teilen die Kreaturen Eigenschaften; Außerhalb der Überlappungen haben die Kreaturen unterschiedliche Eigenschaften.

Bearbeiten Sie dieses Venn-Diagramm

Bearbeiten Sie dieses Venn-Diagramm

Kostenloses Online-Venn-Diagramm-Tool

Möchten Sie ein Venn-Diagramm online mit einem kostenlosen Tool erstellen?

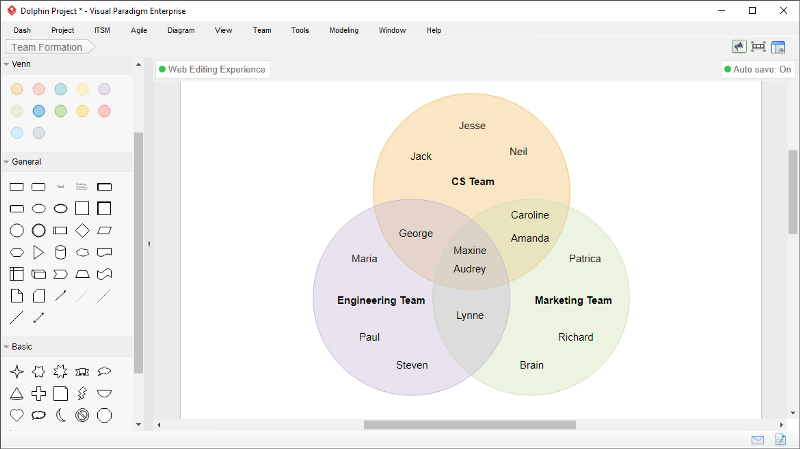
Hier ist eines –  Visual Paradigm Online  ist ein einfaches Diagrammtool, das eine breite Palette von technischen und geschäftlichen Diagrammen unterstützt, einschließlich Venn-Diagrammen.

• Erstellen Sie ein Venn-Diagramm  mit Drag-and-Drop, richten Sie ovale und Textformen präzise aus und legen Sie sie mit der Ausrichtungshilfe fest usw. Es sieht so aus

• Beispielrepository für Venn-Diagramme von VP Online