ベン図：包括的なチュートリアル

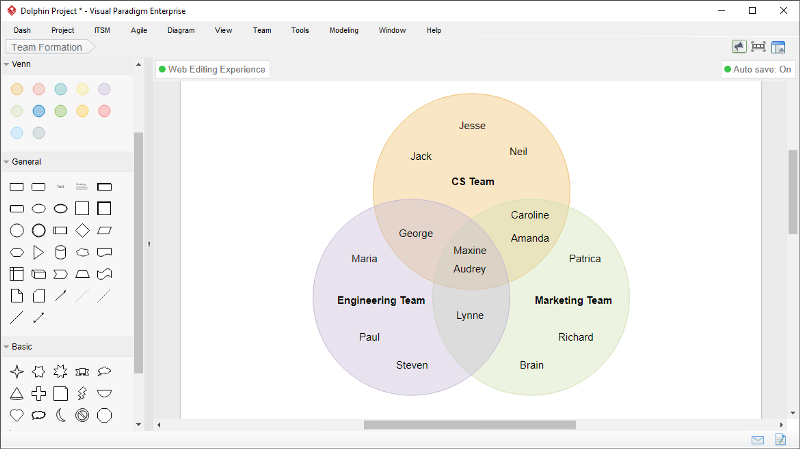
ベン図 は、さまざまなグループ間の関係をグラフまたは図で表したものです。ベン図は、1880年頃にジョンベンによって発明されました。ベン図は、セット図とも呼ばれます。ベン図は、グループまたはセットの論理表現を提供します。2つまたは3つのセット間の関係は、ベン図を使用して簡単に理解できます。数学では、ベン図を使用して、調査、データレポート、および表から取得した既知の情報を分析します。

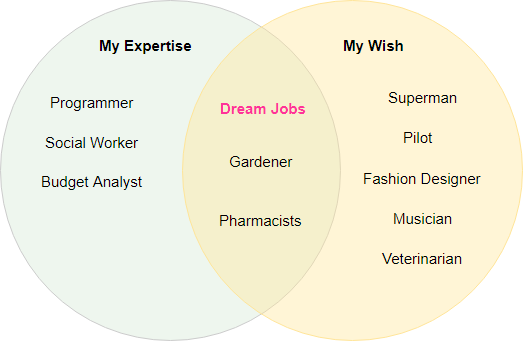
ベン図の目的

• ベン図は、複数のデータセット（通常は2〜4）間の類似点または相違点を表示するのに効果的です。
• ベン図は、いくつかのデータグループを統合した結果も示しています。
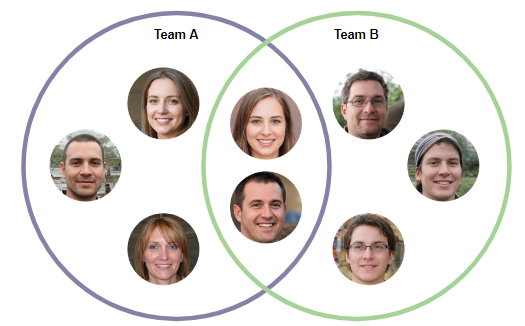
• また、2つの組織/チームの重複する責任についても説明できます。

サークルベン図

ベン図は、円を使用してセットを表し、異なるセットの有限コレクション間の関係を示します。数学では、ベン図を使用して、調査、データレポート、およびそれぞれがセットを表す複数の重なり合う閉じた曲線（通常は円）で構成されるテーブルから取得した既知の情報を分析します。

例えば：

• 自然数のセット= {1,2,3、…..}
• 整数のセット= {0,1,2,3、…..}
• 各オブジェクトは、セットの要素と呼ばれます。

次の例は、ベン図に関連するsetの基本的な操作を示しています。

セットの基本操作Venn図2つのセットA∩B=の共通部分は、セットAとBの両方に存在する要素の数です。

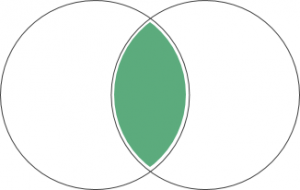
2つのセットの和集合AUB =は、セットAまたはBのいずれかに存在する要素の数です。

2つの対称差

ベン図の例

ベン図の例：学生のクラス

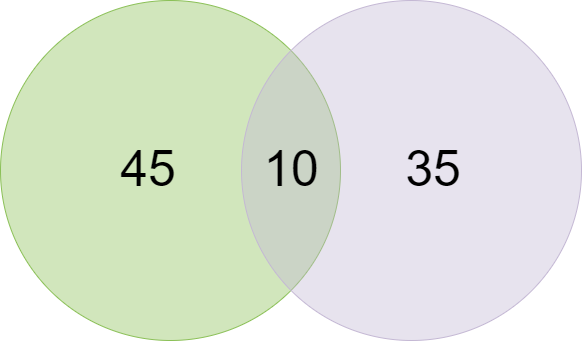
100人の生徒のクラスでは、35人が科学、45人が数学が好きです。両方のように10。どちらかが好きな人とどちらも好きでない人はどれくらいいますか？

• 学生の総数、n（µ）= 100
• 科学の学生の数、n（S）= 35
• 数学の学生の数、n（M）= 45
• 両方が好きな学生の数、n（M∩S）= 10
• どちらかが好きな生徒の数、
• n（MᴜS）= n（M）+ n（S）— n（M∩S）
• →45 + 35–10 = 70
• どちらも好きではない生徒の数= n（µ）— n（MᴜS）= 100–70 = 30

このベン図を編集する

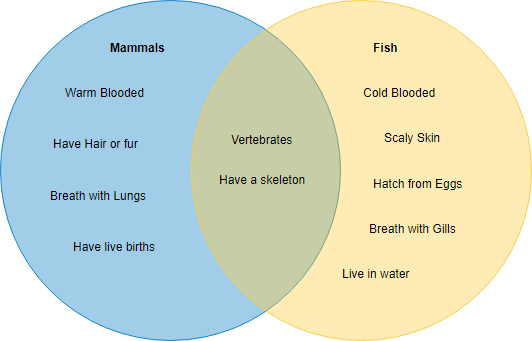
ベン図の例：哺乳類と魚

これは、2つの楕円としてグループ化された哺乳類と魚の特性を示すベン図の例です。共通の特徴は、2つの楕円の重なり合う領域の内側に配置されます。

このベン図を編集する

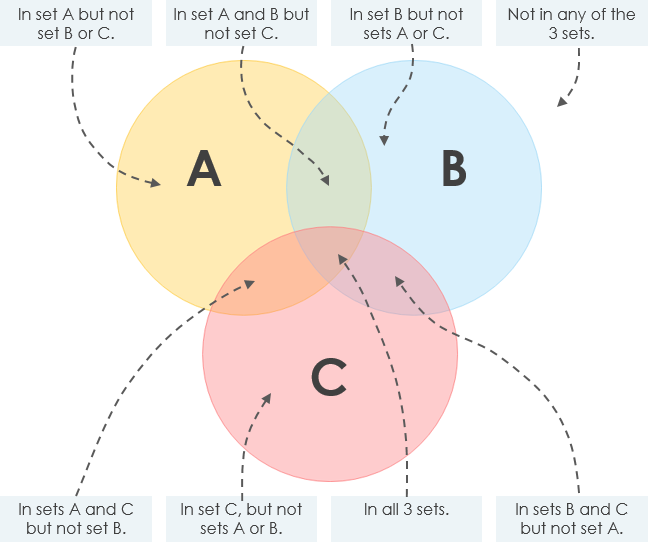
3つの円のベン図

3サークルベン図は、同じプロパティを持つオブジェクトのグループを分類する方法です。

• 互いに交差する3つの円があります。
• 各円には、円に入るものの独自のプロパティのセットがあります。たとえば、奇数や直角の形状などです。
• 円の外側には、どのプロパティにも適合しないオブジェクトが移動できるスペースもあります。
• 次の図は、3つの円を持つベン図がどのように機能するかを示しています。

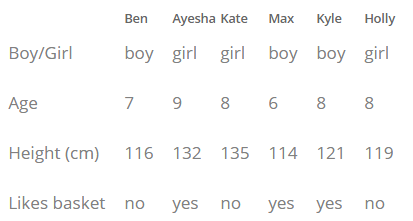
次の例は、上記のセットの概念を示しています。

このベン図を編集する

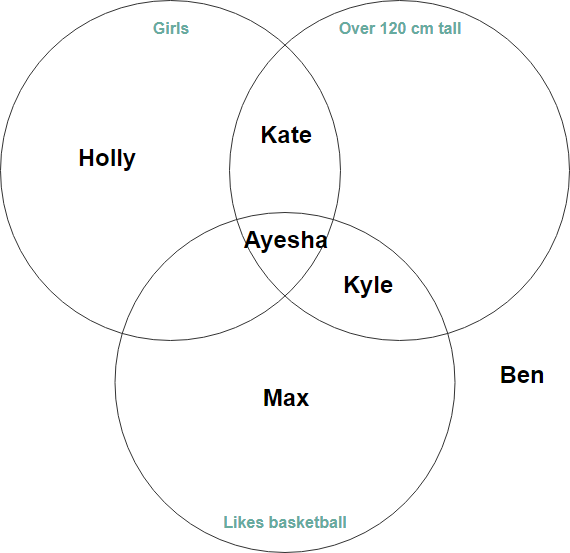
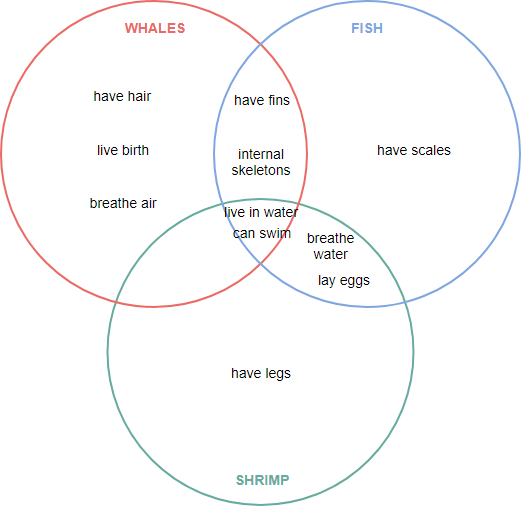
3サークルベン図の例—水生生物

上記の例を拡張することにより、このベン図は、クジラ（哺乳類）と魚、エビ（水生生物）などの水生生物の関係を示すために使用します。さまざまな分野で水生生物の特徴です。オーバーラップでは、クリーチャーはプロパティを共有します。オーバーラップの外側では、クリーチャーは異なるプロパティを持っています。

このベン図を編集する

このベン図を編集する

無料のオンラインベン図ツール

無料のツールを使用してオンラインでベン図を作成したいですか？

これがその1つです—  Visual Paradigm Online は、ベン図を含む幅広い技術図やビジネス図をサポートする簡単な図表作成ツールです。

• ドラッグアンドドロップでベン図 を作成し、配置ガイドなどを使用して楕円形とテキスト形状を正確に配置およびレイアウトします。次のようになります。

• VPOnlineのベン図サンプルリポジトリ