Diagrama de Venn: um tutorial abrangente

Diagramas de Venn  são representações gráficas ou pictóricas de relacionamentos entre diferentes grupos de coisas. O diagrama de Venn foi inventado por John Venn por volta de 1880. Os diagramas de Venn também são chamados de diagramas de conjuntos. Os diagramas de Venn fornecem uma representação lógica dos grupos ou conjuntos. As relações entre dois ou três conjuntos podem ser facilmente compreendidas com a ajuda dos diagramas de Venn. Em matemática, os diagramas de Venn são usados ​​para analisar informações conhecidas obtidas de pesquisas, relatórios de dados e tabelas.

Objetivo dos diagramas de Venn

• Os diagramas de Venn são eficazes na exibição das semelhanças ou diferenças entre vários conjuntos de dados (geralmente dois a quatro).
• Os diagramas de Venn também descrevem o resultado da unificação de vários grupos de dados.
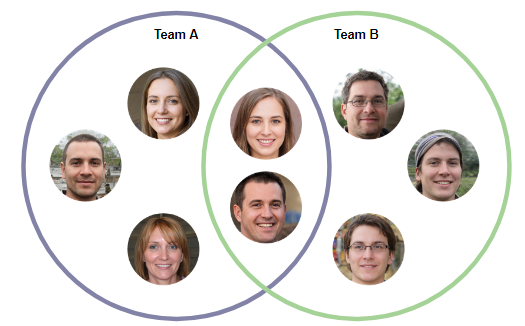
• Eles também podem descrever as responsabilidades sobrepostas de duas organizações/equipes.

Diagramas de Venn do Círculo

Os diagramas de Venn usam círculos para representar conjuntos e ilustrar a relação entre uma coleção finita de conjuntos diferentes. Em matemática, os diagramas de Venn são usados ​​para analisar informações conhecidas obtidas de pesquisas, relatórios de dados e tabelas que consistem em várias curvas fechadas sobrepostas, geralmente círculos, cada um representando um conjunto.

Por exemplo:

• Conjunto de números naturais = {1,2,3,…..}
• Conjunto de números inteiros = {0,1,2,3,…..}
• Cada objeto é chamado de elemento do conjunto.

Os exemplos a seguir mostram as operações básicas de set em relação aos diagramas de Venn.

Diagrama de Venn Operações Básicas de Conjuntos A interseção de dois conjuntos A ∩B = é o número de elementos presentes em ambos os conjuntos A e B.

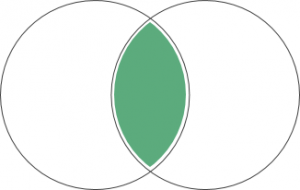
União de dois conjuntos AUB = é o número de elementos presentes em qualquer um dos conjuntos A ou B.

Diferença simétrica de dois

Exemplos de diagramas de Venn

Exemplo de Venn: classe de alunos

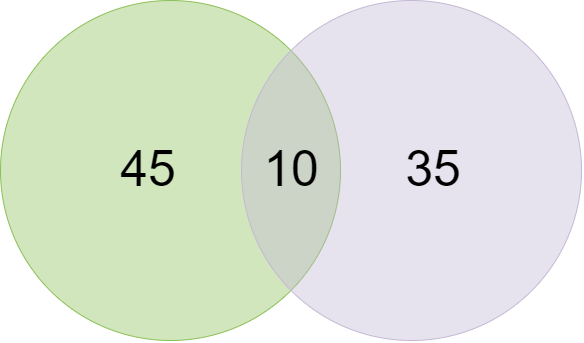
Em uma turma de 100 alunos, 35 gostam de ciências e 45 gostam de matemática. 10 como os dois. Quantos gostam de qualquer um deles e quantos não gostam de nenhum?

• Número total de alunos, n(µ) = 100
• Número de estudantes de ciências, n(S) = 35
• Número de alunos de matemática, n(M) = 45
• Número de alunos que gostam de ambos, n(M∩S) = 10
• Número de alunos que gostam de qualquer um deles,
• n(MᴜS) = n(M) + n(S) — n(M∩S)
• → 45+35–10 = 70
• Número de alunos que não gostam de nenhum = n(µ) — n(MᴜS) = 100–70 = 30

Edite este diagrama de Venn

Exemplo de diagrama de Venn: mamíferos e peixes

Este é um exemplo de diagrama de Venn que mostra as características de mamíferos e peixes, que são agrupados como dois ovais. As características que são comuns são colocadas dentro da região de sobreposição das duas ovais.

Edite este diagrama de Venn

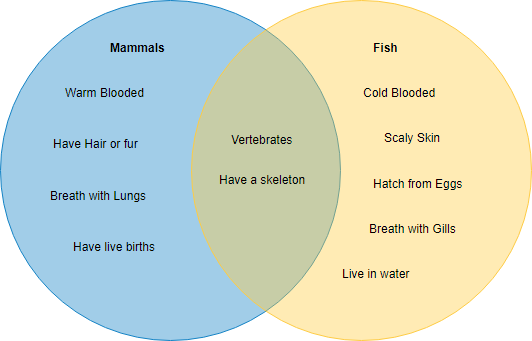
Diagrama de Venn de Três Círculos

Um diagrama de Venn de 3 círculos é uma maneira de classificar grupos de objetos com as mesmas propriedades.

• Tem três círculos que se cruzam.
• Cada círculo tem seu próprio conjunto de propriedades das coisas que entram no círculo, por exemplo, números ímpares ou formas com ângulos retos.
• Há também um espaço fora dos círculos para onde podem ir os objetos que não se encaixam em nenhuma das propriedades.
• O diagrama abaixo mostra como funciona um diagrama de Venn com 3 círculos.

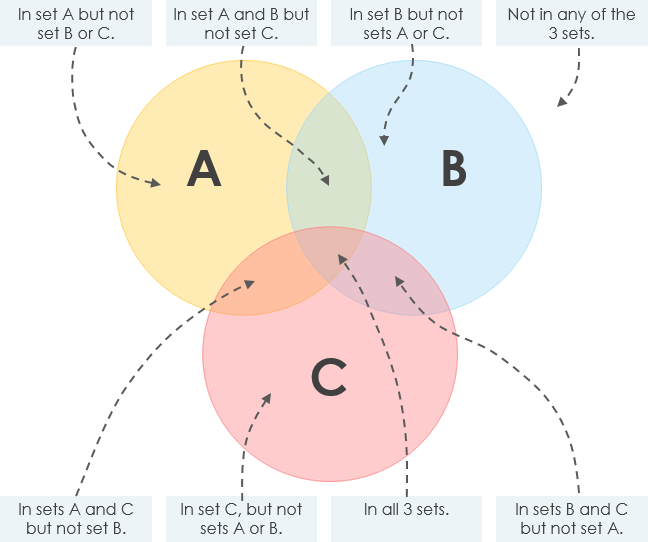
O exemplo a seguir ilustra o conceito do conjunto acima.

Edite este diagrama de Venn

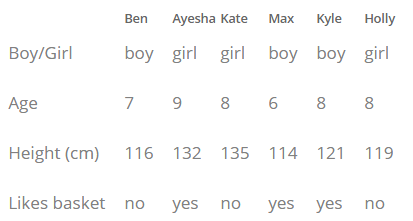
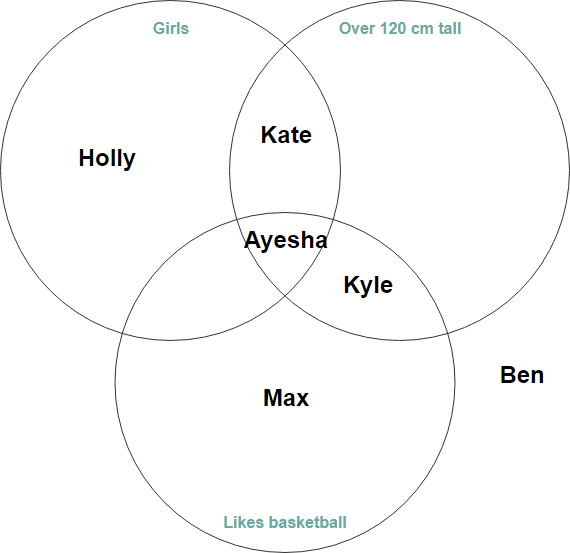
Exemplo de Diagrama de Venn de 3 Círculos – Criaturas Aquáticas

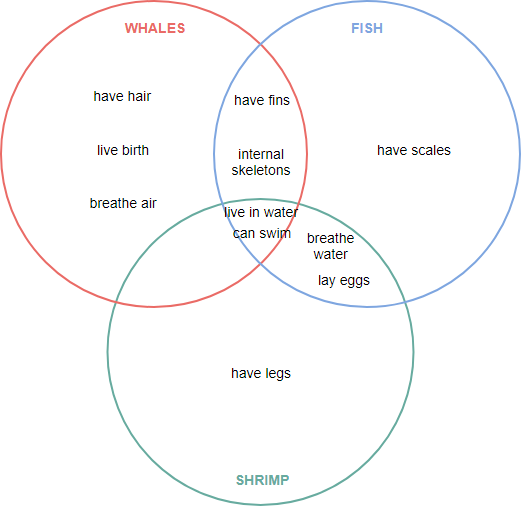
Estendendo o exemplo acima, este diagrama de Venn usa para mostrar as relações entre as formas de vida aquáticas: baleias (mamíferos) e peixes, camarões (criaturas aquáticas). Nos vários campos são características das criaturas aquáticas. Nas sobreposições, as criaturas compartilham propriedades; fora das sobreposições, as criaturas têm propriedades diferentes.

Edite este diagrama de Venn

Edite este diagrama de Venn

Ferramenta Online Gratuita de Diagrama de Venn

Quer criar diagrama de Venn Online com ferramenta gratuita?

Aqui está um -  Visual Paradigm Online  é uma ferramenta de diagramação fácil que suporta uma ampla gama de diagramas técnicos e de negócios, incluindo diagrama de Venn.

• Crie diagrama de Venn  com arrastar e soltar, alinhar e layout de formas ovais e de texto com precisão com guia de alinhamento, etc.

• • Repositório de exemplo de diagrama de Venn do VP Online