Диаграммы Венна — это графическое или иллюстрированное представление взаимосвязей между различными группами вещей. Диаграмма Венна была изобретена Джоном Венном примерно в 1880 году. Диаграммы Венна также называют диаграммами множеств. Диаграммы Венна дают логическое представление групп или наборов. Отношения между двумя или тремя множествами легко понять с помощью диаграмм Венна. В математике диаграммы Венна используются для анализа известной информации, полученной из опросов, отчетов о данных и таблиц.
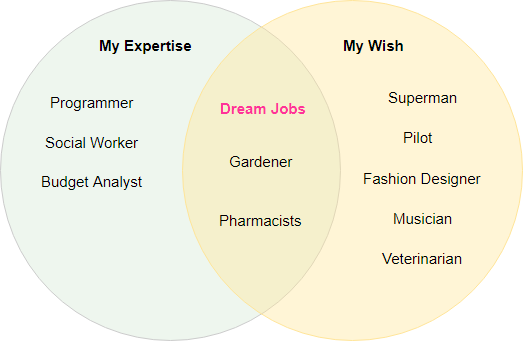
Назначение диаграмм Венна
- Диаграммы Венна эффективны для отображения сходств или различий между несколькими наборами данных (обычно от двух до четырех).
- Диаграммы Венна также описывают результат объединения нескольких групп данных.
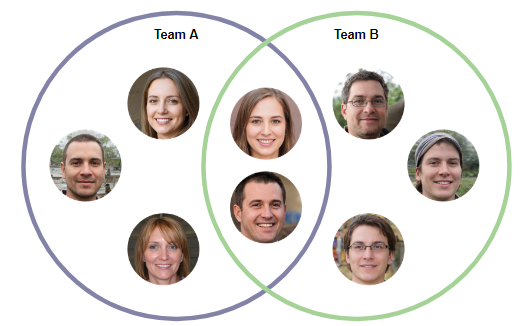
- Они также могут описывать пересекающиеся обязанности двух организаций/команд.
Круговые диаграммы Венна
Диаграммы Венна используют круги для представления множеств и для иллюстрации отношений между конечным набором различных множеств. В математике диаграммы Венна используются для анализа известной информации, полученной из опросов, отчетов о данных и таблиц, состоящих из нескольких перекрывающихся замкнутых кривых, обычно кругов, каждая из которых представляет набор.
Например:
- Набор натуральных чисел = {1,2,3,…..}
- Набор целых чисел = {0,1,2,3,…..}
- Каждый объект называется элементом множества.
В следующих примерах показаны основные операции множества применительно к диаграммам Венна.
Основные операции над множествами Диаграмма Венна Пересечение двух множеств A ∩ B = равно количеству элементов, присутствующих в обоих множествах A и B.
Объединение двух множеств AUB = количество элементов, присутствующих в любом из множеств A или B.

Симметричная разница двух

Примеры диаграммы Венна
Пример Венна: класс студентов
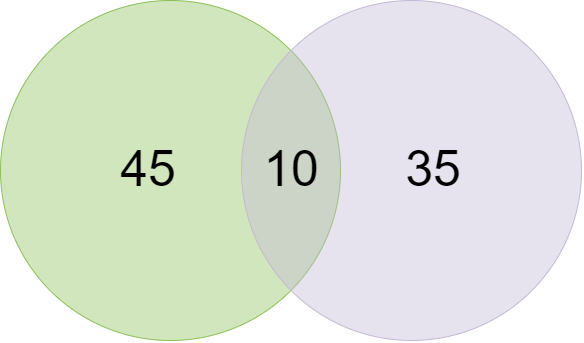
В классе из 100 учеников 35 любят естественные науки и 45 любят математику. 10 нравится обоим. Скольким нравится любой из них и скольким не нравится ни один из них?
- Общее количество студентов, n(µ) = 100
- Количество студентов-естественников, n(S) = 35
- Количество студентов-математиков, n(M) = 45
- Количество студентов, которым нравится и то, и другое, n(M∩S) = 10
- Количество студентов, которым нравится любой из них,
- n(MᴜS) = n(M) + n(S) — n(M∩S)
- → 45+35–10 = 70
- Количество студентов, которым не нравится ни то, ни другое = n(µ) — n(MᴜS) = 100–70 = 30
Пример диаграммы Венна: млекопитающие и рыбы
Это пример диаграммы Венна, на которой показаны характеристики млекопитающих и рыб, сгруппированные в виде двух овалов. Общие характеристики помещаются внутри перекрывающейся области двух овалов.
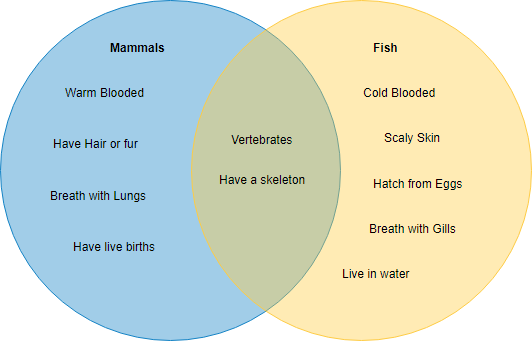
Диаграмма Венна с тремя кругами
Диаграмма Венна с тремя кругами — это способ классификации групп объектов с одинаковыми свойствами.
- Он состоит из трех окружностей, которые пересекаются друг с другом.
- Каждый круг имеет свой собственный набор свойств вещей, которые входят в круг, например, нечетные числа или формы с прямыми углами.
- Также есть пространство за пределами кругов, куда могут попасть объекты, не соответствующие ни одному из свойств.
- На приведенной ниже диаграмме показано, как работает диаграмма Венна с 3 кругами.
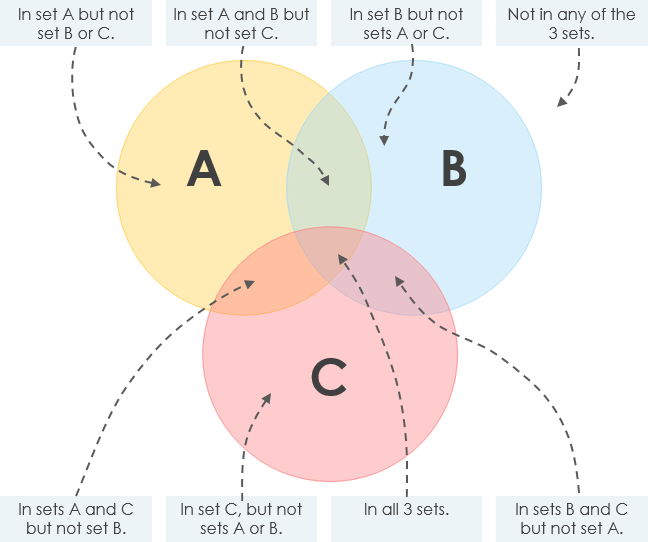
Следующий пример иллюстрирует концепцию набора выше.
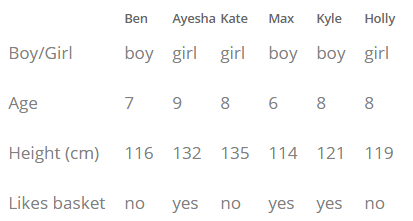
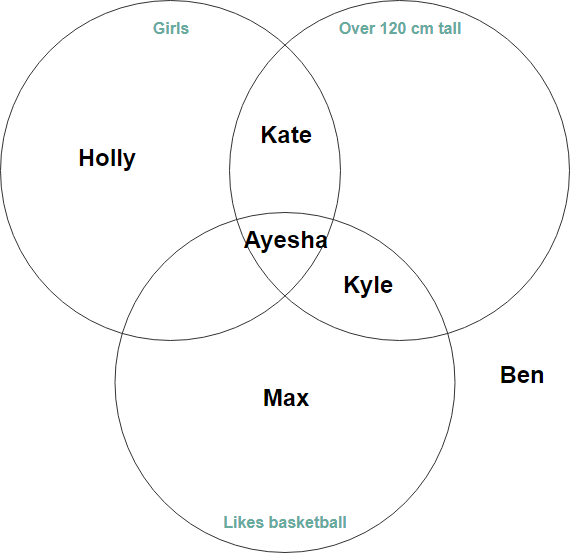
3 Пример круговой диаграммы Венна — водные существа
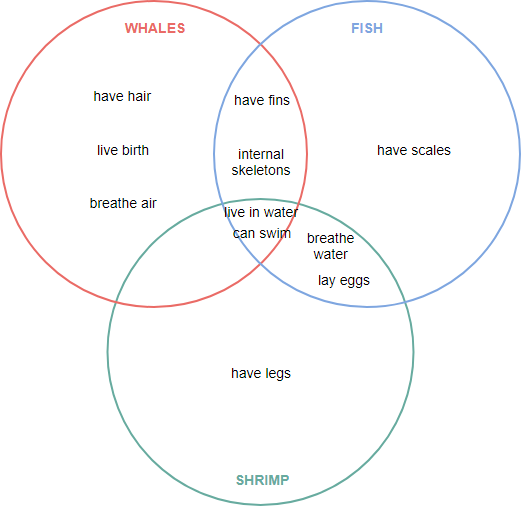
Расширяя приведенный выше пример, эта диаграмма Венна используется для отображения отношений между водными формами жизни: китами (млекопитающие) и рыбами, креветками (водными существами). В различных областях характерны водные существа. В перекрытиях существа имеют общие свойства; вне перекрытий существа имеют разные свойства.
Бесплатный онлайн-инструмент для построения диаграмм Венна
Хотите создать диаграмму Венна онлайн с помощью бесплатного инструмента?
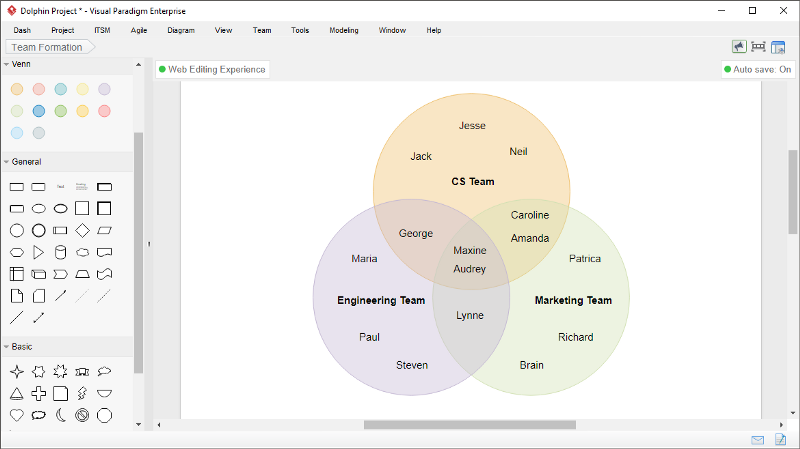
Вот один из них: Visual Paradigm Online — это простой инструмент для построения диаграмм, который поддерживает широкий спектр технических и бизнес-диаграмм, включая диаграмму Венна.
- Создавайте диаграмму Венна с помощью перетаскивания, выравнивайте и размещайте овалы и текстовые фигуры точно с помощью направляющей для выравнивания и т. д. Это выглядит так:
Эта статья также доступна на Deutsch, English, Español, فارسی, Français, Bahasa Indonesia, 日本語, Polski, Portuguese, Việt Nam, 简体中文 and 繁體中文













